高中数学一轮复习《解析几何中的存在性问题》(课件+导学案+教案+教学反思,5份打包)
《解析几何中的存在性问题》公开课教学反思.doc
解析几何中的探究型存在性问题(教案).doc
解析几何中的探究型存在性问题(学案).doc
解析几何中的探究型存在性问题.gsp
解析几何中的探究型存在性问题.ppt
《解析几何中的存在性问题》公开课教学反思
解析几何题向来都是学生心目中的难题.为了帮助学生克服困难,教师自己先要下功夫去研究问题的理论本质、命题背景.我认为,教师应当在教学中选用尽量简单的例子把问题的本质讲透,然后再用典型的例题让学生理清知识脉络、归纳方法、积累经验,内化为自己的知识与方法,在遇到新的问题时会思考、分析并解决.
在《解析几何中的存在性问题》公开课后,我作出了以下几点反思:
一、好的地方
1.学生有较为充足的时间练习并向其他同学展示自己的结果,体现了学生在学习过程中的主体性。
2.学生在练习过程中,我不断巡视学生的情况,对部分学生作出了适当的提点,体现了教师在教学过程中的主导型以及课堂掌控能力。
3.我在巡视过程中,选定了几位同学上台叙述自己的思路并展示自己的成果,之后我再作出点评,无论是台上的同学还是台下的同学都有收获,师生互动非常充分。
4.我在教学中投入了更大的激情,带动了学生的学习热情。
二、不足之处
1.投影设备有故障,在用投影展示学生的解答时,屏幕不时闪烁,影响学生和听课老师的观看。
解析几何中的探究型存在性问题
佛山一中 李维
2015年5月
一、方法回顾与归纳
下面是一些我们曾经做过的探究型存在性问题,你还记得我们是怎样入手来思考并解决这些问题的吗?
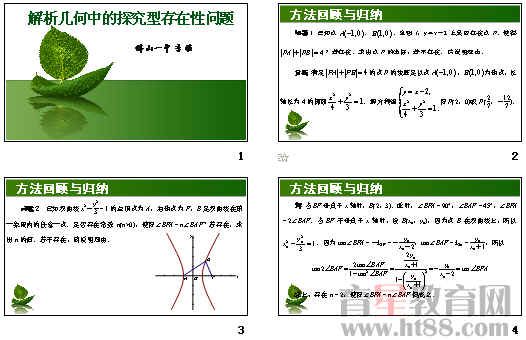
问题1 已知点 , ,直线l:y=x-2上是否存在点P,使得 ?若存在,求出点P的坐标;若不存在,请说明理由.
问题2 已知双曲线x2-y23=1的左顶点为A,右焦点为F,B是双曲线在第一象限内的任意一点.是否存在常数n(n>0),使得∠BFA=n∠BAF?若存在,求出n的值;若不存在,请说明理由.
对于解析几何中的探究型存在性问题,我们一般有如下的解决方法:
1.____________________
2.____________________
3.____________________
二、典型例题
例1 (2008广东文理18)设A、B分别是椭圆 长轴的左、右端点,试探究在抛物线 上是否存在点P,使得△ABP为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
例2 x轴上是否存在异于点P(2,0)定点M,使得以椭圆E:x2+3y2=4的任意一条过点M的弦AB为直径的圆都过点P?若存在,求出点M的坐标;若不存在,请说明理由.
解析几何中的存在性问题
佛山一中 李维
2015年5月
【学情分析】
这是高三(9)班最后一节数学课.高三(9)班的同学经过近一年的复习备考,处理解析几何问题的能力已经有了很大的提高.但是,有部分同学的自信心不足,不敢挑战解析几何题;有不少同学的运算求解能力还不够强.
【教学目的】
1. 掌握解决探究型存在性问题的几种方法;
2. 提高逻辑推理能力与运算求解能力,培养解决解析几何问题的自信;
3. 体会从特殊到一般的数学思想方法.
【教学重难点】
1. 重点:解决探究型存在性问题的几种方法.
2. 难点:代数运算求解.
【教学过程】
一、方法回顾与归纳
回顾学生曾经做过的探究型存在性问题,归纳解题方法.
问题1 已知点 , ,直线l:y=x-2上是否存在点P,使得 ?若存在,求出点P的坐标;若不存在,请说明理由.
分析 满足 的点P的轨迹是以点 , 为焦点,长轴长为4的椭圆 .直线l:y=x-2过椭圆的右顶点(2,0),与椭圆相交.解方程组 得P(2,0)或P (27,-127).
由此,我们可以归纳出解决存在性问题的第一种方法——构造轨迹求交点:在探究点的存在性时,可以从该点满足的部分条件入手,构造该点所在的轨迹曲线,再研究这些曲线的交点.





